Non-Parametric Operational Modal Analysis Methods in Frequency Domain: A Systematic Review
DOI:
https://doi.org/10.46604/ijeti.2021.6126Keywords:
operational modal analysis, peak picking, frequency domain decomposition, enhanced frequency domain decomposition, frequency–spatial domain decompositionAbstract
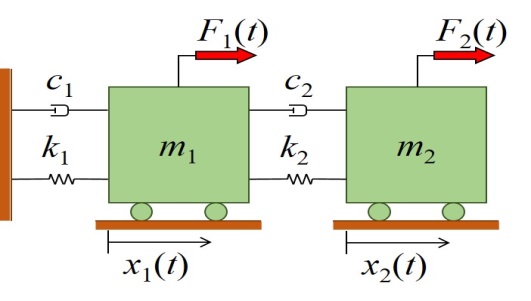
The objective of this research is to present a systematic review of the non-parametric modal analysis methods in the frequency domain. Peak picking (PP), frequency domain decomposition (FDD), enhanced frequency domain decomposition (EFDD), and frequency–spatial domain decomposition (FSDD) are revisited and didactically illustrated by means of modal identification for a study case proposed in previous researches. Algorithm schemes are illustrated to summarize these frequency domain OMA techniques. Modal frequencies, modal damping ratios, and modal shapes are estimated using the different OMA techniques and compared to estimations obtained by the free decay (FD) method reported in previous researches. These are employed to compare the results obtained by the methods presented herein and show a very good correlation in obtaining modal frequencies and a low correlation in the case of modal damping.
References
J. Debille, S. Pauwels, and B. Peeters, “The Benefits of Operational Modal Analysis of Aircraft and Spacecraft Structures,” European Test & Telemetry Conference (ETTC 2005), June 2005, pp. 1-6.
B. Peeters and G. De Roeck, “Stochastic System Identification for Operational Modal Analysis: A Review,” Journal of Dynamic Systems, Measurement, and Control, vol. 123, no. 4, pp. 659-667, December 2001.
M. H. Masjedian and M. Keshmiri, “A Review on Operational Modal Analysis Researches: Classification of Methods and Applications,” 3rd International Operational Modal Analysis Conference (IOMAC 2009), May 2009, pp. 707-716.
R. Brincker and C. E. Ventura, Introduction to Operational Modal Analysis, Hoboken, New Jersey: John Wiley & Sons, 2015.
Z. Xia, T. Wang, and L. Zhang, “Detection and Removal of Harmonic Components in Operational Modal Analysis,” Journal of Vibroengineering, vol. 19, no. 7, pp. 5278-5289, November 2017.
G. Morteza and S. Ahmad, “Operational Modal Analysis Techniques and their Theoreticals and Practical Aspect: A Comprehensive Review and Introduction,” 6th International Operational Modal Analysis Conference (IOMAC 2015), May 2015, pp. 1-16.
G. Zini, M. Betti, G. Bartoli, and S. Chiostrini, “Frequency vs Time Domain Identification of Heritage Structures,” Procedia Structural Integrity, vol. 11, pp. 460-469, 2018.
B. Peeters, T. De Troyer, P. Guillaume, and H. Van der Auweraer, “In-Flight Modal Analysis-A Comparison Between Sweep and Turbulence Excitation,” International Conference on Noise and Vibration Engineering (ISMA2006), September 2006, pp. 1627-1642.
A. De Vivo, C. Brutti, and J. L. Leofanti, “Vega In-Flight Modal Identification with the Operational Modal Analysis Technique,” Journal of Spacecraft and Rockets, vol. 51, no. 5, pp. 1464-1473, September 2014.
B. Peeters, S. Manzato, and H. Van der Auweraer, “Solutions to Deal with Harmonics and Noise for Helicopter in-Flight Data Dynamic Identification,” 5th International Operational Modal Analysis Conference (IOMAC 2013), May 2013, pp. 1-8.
G. James and T. Carne, “Damping Measurements on Operating Wind Turbines Using the Natural Excitation Technique (NExT),” 11th ASME Wind Energy Symposium, January 1992, pp. 75-81.
M. A. Anuar, A. A. M. Isa, A. R. Zamri, and R. Brincker, “Critical Experimental Issues of Cracked Aluminum Beam in Operational Modal Analysis,” Journal of Mechanical Engineering, vol. 15, no. SI 2018 Vol 5-6, pp. 211-225, 2018.
E. P. Carden and M. Lindblad, “Operational Modal Analysis of Torsional Modes in Rotating Machinery,” Journal of Engineering for Gas Turbines and Power, vol. 137, no. 2, pp. 022501 (7 pages), February 2015.
E. P. Carden, “Investigation of Offshore Diesel Generator Failure Using Operational Modal Analysis,” 5th International Operational Modal Analysis Conference (IOMAC 2013), May 2013, pp. 1-10.
M. Karlsson, H. Samuelsson, and M. Karlberg, “Using Operational Modal Analysis to Determine Rotordynamic Modes,” 13th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery (ISROMAC-13), April 2010, pp. 527-530.
A. Mironov, P. Doronkin, A. Priklonsky, and I. Kabashkin, “Operational Modal Analysis (OMA) Application for Condition Monitoring of Operating Pipelines,” Transport and Telecommunication Journal, vol. 16, no. 4, pp. 305-319, 2015.
H. Shokravi, H. Shokravi, N. Bakhary, S. S. Rahimian Koloor, and M. Petrů, “Health Monitoring of Civil Infrastructures by Subspace System Identification Method: An Overview,” Applied Sciences, vol. 10, no. 8, pp. 1-29, 2020.
A. Bajric, R. Brincker, and C. T. Georgakis, “Evaluation of Damping Using Time Domain OMA Techniques,” 2014 SEM Fall Conference and International Symposium on Intensive Loading and Its Effects, October 2014, pp. 1-6.
S. K. Au, “Bayesian Operational Modal Analysis,” Identification Methods for Structural Health Monitoring, Berlin: Springer, 2016.
E. Reynders, “System Identification Methods for (Operational) Modal Analysis: Review and Comparison,” Archives of Computational Methods in Engineering, vol. 19, no. 1, pp. 51-124, March 2012.
H. Cai, P. Du, H. Liu, J. Guo, and Y. Gao, “Modal Analysis of Drive Axle Based on OMA Time Domain Method Identification,” International Conference on Electric Information and Control Engineering (ICEICE 2011), April 2011, pp. 2323-2328.
P. Stoica and R. Moses, Spectral Analysis of Signals, Upper Saddle River, New Jersey: Prentice Hall, 2005.
J. Asmussen, “Modal Analysis Based on the Random Decrement Technique,” Ph.D. dissertation, Department of Mechanical Engineering, Aalborg University, Aalborg, Denmark, 1997.
G. H. James, T. G. Carne, J. P. Lauffer, and A. R. Nord, “Modal Testing Using Natural Excitation,” 10th International Modal Analysis Conference, February 1992, pp. 1209-1216.
A. Felber, “Development of a Hybrid Bridge Evaluation System,” Ph.D. dissertation, Department of Civil Engineering, The University of British Columbia, Vancouver, Canada, 1994.
G. James, T. Carne, and P. Lauffer, “The Natural Excitation Technique (NExT) for Modal Parameter Extraction from Operating Wind Turbines,” Sandia National Laboratories, Technical Report SAND-92-1666, February 01, 1993.
J. S. Bendat, “Spectral Techniques for Nonlinear System Analysis and Identification,” Shock and Vibration, vol. 1, no. 1, pp. 21-31, 1993.
J. S. Bendat and A. G. Piersol, Random Data, Analysis and Measurement Procedures, 4th ed. New York: John Wiley & Sons, 2010.
R. Brincker, L. Zhang, and P. Andersen, “Modal Identification from Ambient Responses Using Frequency Domain Decomposition,” International Modal Analysis Conference (IMAC 18), February 2000, pp. 625-630.
R. Brincker, C. E. Ventura, and P. Andersen, “Damping Estimation by Frequency Domain Decomposition,” International Modal Analysis Conference (IMAC 19), February 2001, pp. 698-703.
R. Brincker and P. Andersen, Method for Vibration Analysis, U.S. Patent US 6,779,404 B1, August 24, 2004.
Y. Zhang, Z. Zhang, X. Xu, and H. Hua, “Modal Parameter Identification Using Response Data Only,” Journal of Sound and Vibration, vol. 282, no. 1-2, pp. 367-380, April 2005.
L. Zhang, T. Wang, and Y.Tamura “A Frequency–Spatial Domain Decomposition (FSDD) Technique for Operational Modal Analysis,” Mechanical Systems and Signal Processing, vol. 24, no. 5, pp. 1227-1239, July 2010.
T. Wang, O. Celik, F. N. Catbas, and L. M. Zhang, “A Frequency and Spatial Domain Decomposition Method for Operational Strain Modal Analysis and Its Application,” Engineering Structures, vol. 114, pp. 104-112, May 2016.
P. Andersen, R. Brincker, B. Peeters, G. De Roeck, L. Hermans, and C. Krämer, “Comparison of System Identification Methods Using Ambient Bridge Test Data,” International Modal Analysis Conference (IMAC 17), February 1999, pp. 1035-1041.
M. Batel, “Operational Modal Analysis - Another Way of Doing Modal Testing,” Sound and Vibration, vol. 36, no. 8, pp. 22-27, August 2002.
C. Devriendt and P. Guillaume, “Identification of Modal Parameters from Transmissibility Measurements,” Journal of Sound and Vibration, vol. 314, no. 1-2, pp. 343-356, July 2008.
S. Gade, N. B. Møller, H. Herlufsen, and H. Konstantin-Hansen, “Frequency Domain Techniques for Operational Modal Analysis,” 1st International Operational Modal Analysis Conference (IOMAC 2005), May 2005, pp. 261-271.
F. Magalhães, R. Brincker, and Á. Cunha, “Damping Estimation using Free Decays and Ambient Vibration Tests,” 2nd International Operational Modal Analysis Conference (IOMAC 2007), May 2007, pp. 513-521.
S. S. Rao, Mechanical Vibrations, 5th ed. New York: Prentice-Hall, 2011.
P. Verboven, “Frequency-Domain System Identification for Modal Analysis,” Ph.D. dissertation, Department of Mechanical Engineering, Vrije Universiteit Brussel, Brussels, Belgium, 2002.
P. Guillaume, P. Verboven, and S. Vanlanduit, “Frequency-Domain Maximum Likelihood Identification of Modal Parameters with Confidence Intervals,” International Seminar on Modal Analysis, September 1998, pp. 359-366.
Published
How to Cite
Issue
Section
License
Copyright Notice
Submission of a manuscript implies: that the work described has not been published before that it is not under consideration for publication elsewhere; that if and when the manuscript is accepted for publication. Authors can retain copyright in their articles with no restrictions. Also, author can post the final, peer-reviewed manuscript version (postprint) to any repository or website.

Since Jan. 01, 2019, IJETI will publish new articles with Creative Commons Attribution Non-Commercial License, under Creative Commons Attribution Non-Commercial 4.0 International (CC BY-NC 4.0) License.
The Creative Commons Attribution Non-Commercial (CC-BY-NC) License permits use, distribution and reproduction in any medium, provided the original work is properly cited and is not used for commercial purposes.






.jpg)


