A Recursive Least-Squares Approach with Memorizing Factor for Deriving Dynamic Equivalents of Power Systems
DOI:
https://doi.org/10.46604/aiti.2021.7853Keywords:
network reduction, transient stability, critical clearing time, system identificationAbstract
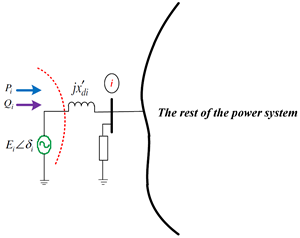
In this research, a two-stage identification-based approach is proposed to obtain a two-machine equivalent (TME) system of an interconnected power system for transient stability studies. To estimate the parameters of the equivalent system, a three-phase fault is applied near and/or at the bus of a local machine in the original multimachine system. The electrical parameters of the equivalent system are calculated in the first stage by equating the active and reactive powers of the local machine in both the original and the predefined equivalent systems. The mechanical parameters are estimated in the second stage by using a recursive least-squares estimation (RLSE) technique with a factor called “memorizing factor”. The approach is demonstrated on New England 10-machine 39-bus system, and its accuracy and efficiency are verified by computer simulation in MATLAB software. The results obtained from the TME system agree well with those obtained from the original multimachine system.
References
J. Machowski, Z. Lubosny, J. Bialek, and J. R. Bumby, Power System Dynamics: Stability and Control, 3rd ed. Hoboken: John Wiley & Sons, 2020.
A. Karami and K. M. Galougahi, “Improvement in Power System Transient Stability by Using STATCOM and Neural Networks,” Electrical Engineering, vol. 101, no. 1, pp. 19-33, April 2019.
E. C. Machado and J. E. Pessanha, “Foundations on the Hamiltonian Energy Balance Method for Power System Transient Stability Analysis: Theory and Simulation,” Journal of Control, Automation, and Electrical Systems, vol. 31, no. 1, pp. 226-232, February 2020.
Y. F. Gao, J. Q. Wang, T. N. Xiao, and D. Z. Jiang, “Fast Emergency Control Strategy Calculation Based on Dynamic Equivalence and Integral Sensitivity,” Frontiers of Information Technology and Electronic Engineering, vol. 20, no. 8, pp. 1119-1132, August 2019.
X. Y. Li and O. P. Malik, “Estimation of Equivalent Models for Emergency State Control of Interconnected Power-Systems Based on Multistage Recursive Least-Squares Identification,” IEE Proceedings C (Generation, Transmission, and Distribution), vol. 140, no. 4, pp. 319-325, July 1993.
J. B. Ward, “Equivalent Circuits for Power-Flow Studies,” Transactions of the American Institute of Electrical Engineers, vol. 68, no. 1, pp. 373-382, July 1949.
P. Dimo, Nodal Analysis of Power Systems, Lancashire: Abacus Press, 1975.
J. Srivani and K. S. Swarup, “Power System Static Security Assessment and Evaluation Using External System Equivalents,” International Journal of Electrical Power and Energy Systems, vol. 30, no. 2, pp. 83-92, February 2008.
Y. Fu and T. S. Chung, “A Hybrid Artificial Neural Network (ANN) and Ward Equivalent Approach for On-Line Power System Voltage Security Assessment,” Electric Power System Research, vol. 53, no. 3, pp. 165-171, March 2000.
B. G. Lee, J. Lee, and S. Kim, “Development of a Static Equivalent Model for Korean Power Systems Using Power Transfer Distribution Factor-Based k-Means++ Algorithm,” Energies, vol. 13, no. 24, 6663, December 2020.
U. D. Annakkage, N. K. C. Nair, Y. Liang, A. M. Gole, V. Dinavahi, B. Gustavsen, et al., “Dynamic System Equivalents: A Survey of Available Techniques,” IEEE Transactions on Power Delivery, vol. 27, no. 1, pp. 411-420, January 2012.
J. H. Chow, Power System Coherency and Model Reduction, Springer Science and Business Media, 2013.
M. R. A. Paternina, J. M. Ramirez-Arredondo, J. D. Lara-Jiménez, and A. Zamora-Mendez, “Dynamic Equivalents by Modal Decomposition of Tie-Line Active Power Flows,” IEEE Transactions on Power Systems, vol. 32, no. 2, pp. 1304-1314, March 2017.
C. M. Rergis, R. J. Betancourt, and A. R. Messina, “Order Reduction of Power Systems by Modal Truncated Balanced Realization,” Electric Power Components and Systems, vol. 45, no. 2, pp. 147-158, 2017.
D. Chaniotis and M. A. Pai, “Model Reduction in Power Systems Using Krylov Subspace Methods,” IEEE Transactions on Power Systems, vol. 20, no. 2, pp. 888-894, May 2005.
Z. Zhu, G. Geng, and Q. Jiang, “Power System Dynamic Model Reduction Based on Extended Krylov Subspace Method,” IEEE Transactions on Power Systems, vol. 31, no. 6, pp. 4483-4494, November 2016.
T. K. Ritschel, F. Weiß, M. Baumann, and S. Grundel, “Nonlinear Model Reduction of Dynamical Power Grid Models Using Quadratization and Balanced Truncation,” Automatisierungstechnik, vol. 68, no. 12, pp. 1022-1034, November 2020.
R. Podmore, “Identification of Coherent Generators for Dynamic Equivalents,” IEEE Transactions on Power Apparatus and Systems, vol. 97, no. 4, pp. 1344-1354, July 1978.
J. J. Ayon, E. Barocio, I. R. Cabrera, and R. Betancourt, “Identification of Coherent Areas Using a Power Spectral Density Algorithm,” Electrical Engineering, vol. 100, no. 2, pp. 1009-1019, June 2018.
A. M. Miah, “Study of a Coherency-Based Simple Dynamic Equivalent for Transient Stability Assessment,” IET Generation, Transmission, and Distribution, vol. 5, no. 4, pp. 405-416, April 2011.
M. Matar, N. Fernandopulle, and A. Maria, “Dynamic Model Reduction of Large Power Systems Based on Coherency Aggregation Techniques and Black-Box Optimization,” International Conference on Power Systems Transients, June 2013, pp. 1-7.
S. Chittora and S. N. Singh, “Coherency Based Dynamic Equivalencing of Electric Power System,” 18th National Power Systems Conference, December 2014, pp. 1-6.
A. M. Stankovic, A. T. Saric, and M. Milosevic, “Identification of Nonparametric Dynamic Power System Equivalents with Artificial Neural Networks,” IEEE Transactions on Power Systems, vol. 18, no. 4, pp. 1478-1486, November 2003.
A. Chakrabortty and A. Salazar, “Building a Dynamic Electro-Mechanical Model for the Pacific AC Intertie Using Distributed Synchrophasor Measurements,” European Transactions on Electrical Power, vol. 21, no. 4, pp. 1657-1672, May 2011.
J. M. Ramirez, B. V. Hernández, and R. E. Correa, “Dynamic Equivalence by an Optimal Strategy,” Electric Power System Research, vol. 84, no. 1, pp. 58-64, March 2012.
J. L. Rueda, J. Cepeda, I. Erlich, D. Echeverría, and G. Argüello, “Heuristic Optimization Based Approach for Identification of Power System Dynamic Equivalents,” International Journal of Electrical Power and Energy Systems, vol. 64, pp. 185-193, January 2015.
X. Zhang, Y. Xue, S. You, Y. Liu, Z. Yuan, J. Chai, et al., “Measurement-Based Power System Dynamic Model Reductions,” North American Power Symposium, September 2017, pp. 1-6.
N. Tong, Z. Jiang, S. You, L. Zhu, X. Deng, Y. Xue, et al., “Dynamic Equivalence of Large-Scale Power Systems Based on Boundary Measurements,” American Control Conference, July 2020, pp. 3164-3169.
Z. Jiang, N. Tong, Y. Liu, Y. Xue, and A. G. Tarditi, “Enhanced Dynamic Equivalent Identification Method of Large-Scale Power Systems Using Multiple Events,” Electric Power Systems Research, vol. 189, 106569, December 2020.
A. B. Almeida, R. Reginatto, and R. J. G. C. D. Silva, “A Software Tool for the Determination of Dynamic Equivalents of Power Systems,” IREP Symposium Bulk Power System Dynamics and Control, August 2010, pp. 1-10.
K. J. Keesman, System Identification: An Introduction, London: Springer, 2011.
M. A. Pai, Energy Function Analysis for Power System Stability, Boston: Kluwer Academic Publishers, 1989.
R. D. Zimmerman, C. E. Murillo-Sánchez, and R. J. Thomas, “MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education,” IEEE Transactions on Power Systems, vol. 26, no. 1, pp. 12-19, February 2011.
A. Karami and S. Z. Esmaili, “Transient Stability Assessment of Power Systems Described with Detailed Models Using Neural Networks,” International Journal of Electrical Power and Energy Systems, vol. 45, no. 1, pp. 279-292, February 2013.
A. Slowik, Swarm Intelligence Algorithms: A Tutorial, Boca Raton: CRC Press, 2021.
Published
How to Cite
Issue
Section
License
Submission of a manuscript implies: that the work described has not been published before that it is not under consideration for publication elsewhere; that if and when the manuscript is accepted for publication. Authors can retain copyright in their articles with no restrictions. is accepted for publication. Authors can retain copyright of their article with no restrictions.
Since Jan. 01, 2019, AITI will publish new articles with Creative Commons Attribution Non-Commercial License, under The Creative Commons Attribution Non-Commercial 4.0 International (CC BY-NC 4.0) License.
The Creative Commons Attribution Non-Commercial (CC-BY-NC) License permits use, distribution and reproduction in any medium, provided the original work is properly cited and is not used for commercial purposes.







