A Direct Lyapunov-Backstepping Approach for Stabilizing Gantry Systems with Flexible Cable
Keywords:
flexible systems, overhead crane, field oriented control, Lyapunov direct methodAbstract
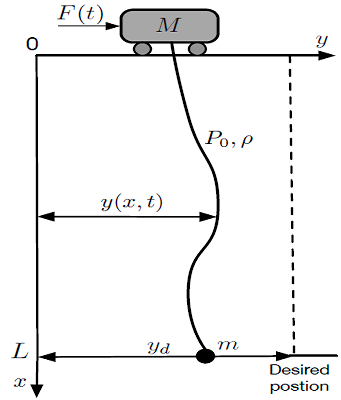
Trolley positioning and payload swinging control problem of a flexible cable gantry crane system are addressed in this paper. The system’s equations of motion that couple the crane’s cable and actuators dynamics are derived via extended Hamilton’s principle. The control signal is designed based on the Lyapunov direct method to derive control force and backstepping technique is employed to determine input signal for the actuator. The stability of the closed loop system is proven analytically. Numerical simulations are included to demonstrate the effectiveness and robustness of the closed-loop system.
References
R. Blevins, Formulas for natural frequency and mode shape, New York: Van Nostrand Reinhold Co., 1979.
W. Singhose, D. Kim, and M. Kenison, “Input shaping control of double-pendulum bridge crane oscillations,” Journal of Dynamic Systems, Measurement and Control, vol. 130, no. 3, pp. 1-7, May 2008.
R. Manning, J. Clement, D. Kim, and W. Singhose, “Dynamics and control of bridge cranes transporting distributed-mass payloads,” Journal of Dynamic Systems, Measurement and Control, vol. 132, no. 1, pp. 014-505, January 2010.
D. Kim and W. Singhose, “Performance studies of human operators driving double-pendulum bridge cranes,” Control Engineering Practice, vol. 18, no. 6, pp. 567-576, 2010.
Y. Sakawa and H. Sano, “Nonlinear model and linear robust control of overhead traveling cranes,” Nonlinear Analysis, Theory, Methods & Applications, vol. 30, no. 4, pp. 2197-2207, 1997.
Y. Fang, W. E. Dixon, D. Dawson, and E. Zergeroglu, “Nonlinear coupling control laws for an under-actuated overhead crane system,” IEEE/ASME transactions on mechatronics, vol. 8, no. 3, pp. 418-423, September 2003.
H. Park, D. Chwa, and K. S. Hong, “A feedback linearization control of container cranes: Varying rope length,” International Journal of Control Automation and Systems, vol. 5, no. 4, pp. 379-387, August 2007.
H. H. Lee, “An anti-swing trajectory control of overhead cranes with high-speed hoisting,” Proc. Amer. Control Conf., Denver, June 2003, pp. 1440-1445.
H. H. Lee, “A new approach for the anti-swing control of overhead cranes with high-speed load hoisting,” International Journal of Control, vol. 76, no. 15, pp. 1493-1499, October 2003.
H. H. Lee, Y. Liang, and D. Segura, “A sliding-mode anti-swing trajectory control for overhead cranes with high-speed load hoisting,” Journal of Dynamic Systems Measurement and Control, vol. 128, no. 4, pp. 842-845, December 2006.
H. H. Lee, “Motion planning for three-dimensional overhead cranes with high-speed load hoisting,” International Journal of Control, vol. 78, no. 12, pp. 875-886, August 2005.
J. H. Yang and K. S. Yang, “Adaptive coupling control for overhead crane systems,” Mechatronics, vol. 17, no. 2-3, pp. 143-152, March-April 2007.
J. H. Yang and K. S. Yang, “Adaptive control for 3-D overhead crane systems,” Proc. Amer. Control Conf., June 2006, pp. 1832-1837.
A. T. Le and S. G. Lee, “3D cooperative control of tower cranes using robust adaptive techniques,” Journal of the Franklin Institute, vol. 354, no. 18, pp. 8333-8357, 2017.
A. Benhidjeb and G. L. Gissinger, “Fuzzy control of an overhead crane performance comparison with classic control,” Control Engineering Practice, vol. 3, no. 12, pp. 1687-1696, December 1995.
J. H. Suh, J. W. Lee, Y. J. Lee, and K. S. Lee, “Anti-sway position control of an automated transfer crane based on neural network predictive PID controller,” Journal of Mechanical Science and Technology, vol. 19, no. 2, pp. 505-519, December 2005.
T. A. Le, G. H. Kim, M. Y. Kim, and S. G. Lee, “Partial feedback linearization control of overhead crane with varying cable lengths,” International Journal of Precision Engineering and Manufacturing, vol. 13, no. 4, pp. 501-507, 2012.
N. C. Singer and W. P. Seering, “Preshaping command inputs to reduce system vibration,” Journal of Dynamic Systems, Measurement and Control, vol. 112, no. 1, pp. 76-82, March 1990.
W. Singhose, W. Seering, and N. Singer, “Residual vibration reduction using vector diagrams to generate shaped inputs,” ASME J. of Mechanical Design, vol. 116, no. 2, pp. 654-659, June 1994.
T. Singh and S. R. Vadali, “Robust time-delay control,” Journal of Dynamic Systems, Measurement and Control, vol. 115, no. 2A, pp. 303-306, 1993.
S. Joshi,. “Position control of a flexible cable gantry crane: Theory and Experiment,” Proc. the American Control Conference, June 1995, pp. 2820-2824.
B. D’Andréa-Novel and J. M. Coron, “Exponential stabilization of an overhead crane with flexible cable via a back-stepping approach,” Automatica, vol. 36, no. 4, pp. 587-593, 2000.
G. Lodewijks, “Anti-sway control of container cranes as a flexible cable system,” Proc. IEEE International Conf. Control Applications, IEEE Press, 2004, pp. 1564-1569.
S. S. Ge, S. Zhang, and W. He, “Vibration control of a coupled nonlinear string system in transverse and longitudinal directions,” Proc. the IEEE Conf. Decision and Control, IEEE Press, 2011, pp. 3742-3747.
X. He, W. He, J. Shi, and C. Sun, “Boundary vibration control of variable length crane systems in two-dimensional space with output constraints,” Proc. IEEE/ASME Transactions on Mechatronics, IEEE Press, 2017, vol. 22, no. 5, pp. 1952-1962.
T. L. Nguyen and M. D. Duong, “Nonlinear Control of Flexible Two-Dimensional Overhead Cranes, Adaptive Robust Control Systems,” InTech, DOI: 10.5772/intechopen.71657, 2018.
J. K. Liu, H. Qin, and W. He, “Modelling and vibration control for a flexible string system in three-dimensional space,” IET Control Theory & Applications, vol. 9, no. 16, pp. 2387-2394, 2015.
Published
How to Cite
Issue
Section
License
Submission of a manuscript implies: that the work described has not been published before that it is not under consideration for publication elsewhere; that if and when the manuscript is accepted for publication. Authors can retain copyright of their article with no restrictions. Also, author can post the final, peer-reviewed manuscript version (postprint) to any repository or website.

Since Oct. 01, 2015, PETI will publish new articles with Creative Commons Attribution Non-Commercial License, under The Creative Commons Attribution Non-Commercial 4.0 International (CC BY-NC 4.0) License.
The Creative Commons Attribution Non-Commercial (CC-BY-NC) License permits use, distribution and reproduction in any medium, provided the original work is properly cited and is not used for commercial purposes



