Thermal Analysis of a Cracked Half-plane under Moving Point Heat Source

Authors

  • He Kuanfang Hunan Provincial Key Laboratory of Health Maintenance for Mechanical Equipment, Hunan University of Science and Technology, Xiangtan, Hunan, China 411201
  • Yang Qing
  • Xiao Dongming
  • Li Xuejun

Keywords:

Heat conduction, Moving point heat source, Insulated crack, The moving coordinate method, Singular integral equation, Numerical solution method

Abstract

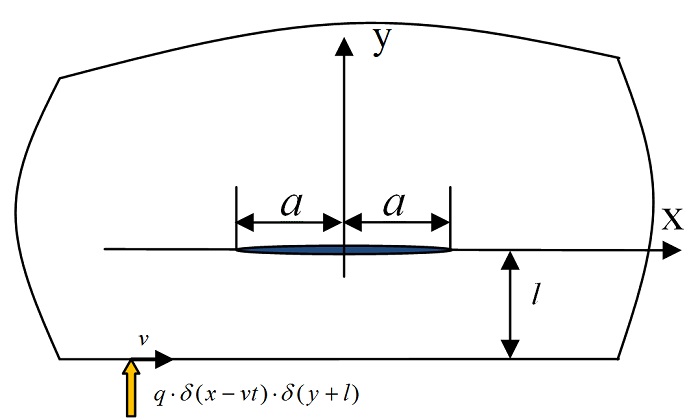
The heat conduction in half-plane with an insulated crack subjected to moving point heat source is investigated. The analytical solution and the numerical means are combined to analyze the transient temperature distribution of a cracked half-plane under moving point heat source. The transient temperature distribution of the half plane structure under moving point heat source is obtained by the moving coordinate method firstly, then the heat conduction equation with thermal boundary of an insulated crack face is changed to singular integral equation by applying Fourier transforms and solved by the numerical method. The numerical examples of the temperature distribution on the cracked half-plane structure under moving point heat source are presented and discussed in detail.

References

X. K. Zhu and Y. J. Chao, “Numerical simulation of transient temperature and residual stresses in friction stir welding of 304L stainless steel,” Journal of Materials Processing Technology, vol. 146, no. 2, pp. 263-272, 2004.

T. Boellinghaus, Hot cracking phenomena in welds, Berlin: Springer, pp. 3-18, 2005.

D. Rosenthal, “The theory of moving sources of heat and its application to metal treatments,” Transactions of The ASME, vol. 68, no. 8, pp. 849-866, 1946.

K. Masubuchi and D. W. Hopkins, Analysis of welded structures, 1st ed. London: Pergamon Press, 1980.

G. M. Oreper and J. Szekely, “Heat and fluid-flow phenomena in weld pools,” Journal of Fluid Mechanics, vol. 147, pp. 53-79, 1984.

R. T. C. Choo, J. Szekely, and R. C. Westhoff, “On the calculation of the free surface temperature of gas-tungsten-arc weld pools from first principles: part I. modeling the welding arc,” Metallurgical Transactions, vol. 23, no. 3, pp. 357-369, 1992.

J. J. Lowke, R. Morrow, and J. Haidar, “A simplified unified theory of arcs and their electrodes,” Journal of Physics D Applied Physics, vol. 30, no. 14, pp. 2033-2042, 1997.

S. Kou and Y. H. Wang, “Computer simulation of convection in moving arc weld pools,” Metallurgical and Materials Transactions A, vol. 17, no. 12, pp. 2271-2277, 1986.

S. D. Kim and S. J. Na, “A study on heat and mass flow in stationary gas tungsten arc welding using the numerical mapping method,” Proc. of the Institution of Mechanical Engineers Part B Journal of Engineering Manufacture, 1989, pp. 233-242.

H. G. Fan and Y. W. Shi, “Numerical simulation of the arc pressure in gas tungsten arc welding,” Journal of Materials Processing Technology, vol. 61, pp. 302-308, 1996.

Y. Joshi, P. Dutta, P. E. Schupp, and D. Espinosa, “Nonaxisymmetric convection in stationary gas tungsten arc weld pools,” Journal of Heat Transfer, vol. 119, no. 1, pp. 164-172, 1997.

M. Tanaka, H. Terasaki, M. Ushio, and J. J. Lowke, “A unified numerical modeling of stationary tungsten-inert-gas welding process,” Metallurgical and Materials Transactions A, vol. 33, no. 7, pp. 2043-2052, 2002.

Y. H. Wei, Z. B. Dong, R. P. Liu, and Z. J. Dong, “Three-dimensional numerical simulation of weld solidification cracking,” Modelling & Simulation in Materials Science & Engineering, vol. 13, no. 3, pp. 437-454, 2005.

J. Hu and H. L. Tsai, “Heat and mass transfer in gas metal arc welding, part I: the arc,” International Journal of Heat and Mass Transfer, vol. 50, pp. 833-846, 2007.

A. H. Yaghi, T. H. Hyde, A. A. Becker, and W. Sun, “Finite element simulation of welding and residual stresses in a P91 steel pipe incorporating solid-state phase transformation and post-weld heat treatment,” The Journal of Strain Analysis for Engineering Design, vol. 43, no. 5, pp. 275-293, 2008.

R. Das, K. S. Bhattacharjee, and S. Rao, “Welding heat transfer analysis using element free galerkin method,” Advanced Materials Research, vol. 410, pp. 298-301, 2011.

M. Sheikhi, F. M. Ghaini, and H. Assadi, “Solidification crack initiation and propagation in pulsed laser welding of wrought heat treatable aluminum alloy,” Science and Technology of Welding and Joining, vol. 19, no. 3, pp. 250-255, 2014.

G. C. Sih, “Heat conduction in the infinite medium with lines of discontinuities,” Journal of Heat Transfer, vol. 87, no. 2, pp. 283-298, 1965.

Y. T. Da, “Characteristics of thermal and flow behavior in the vicinity of discontinuities,” International Journal of Heat and Mass Transfer, vol. 35, no. 2, pp. 481-491, 1992.

N. Noda and Z. H. Jin, “Thermal stress intensity factors for a crack in a strip of a functionally gradient material,” International Journal of Solids and Structures, vol. 30, no. 8, pp. 1039-1056, 1993.

Y. Zhou, X. Li, and D. Yu, “A partially insulated interface crack between a graded orthotropic coating and a homogeneous orthotropic substrate under thermal flux supply,” International Journal of Solids & Structures, vol. 47, no. 6, pp. 768-778, 2010.

Z. H. Jin and N. Naotake, “Transient thermal stress intensity factors for a crack in a semi-infinite plate of a functionally gradient material,” International Journal of Solids and Structures, vol. 31, no. 2, pp. 203-218, 1994.

J. J. Mason and A. J. Rosakis, “On the dependence of the dynamic crack tip temperature fields in metals upon crack tip velocity and material parameters,” Nasa Sti/recon Technical Report N, vol. 93, pp. 337-350, 1992.

C. Y. Chang and C. C. Ma, “Transient thermal conduction of a rectangular plate with multiple insulated cracks by the alternating method,” International Journal of Heat & Mass Transfer, vol. 44, pp. 2423-2437, 2001.

A. Zamani, R. B. Hetnarski, and M. R. Eslami, “Second sound in a cracked layer based on Lord-Shulman theory,” Journal of Thermal Stresses, vol. 34, no. 3, pp. 181-200, 2011.

B. L. Wang and J. C. Han, “A crack in a finite medium under transient non-Fourier heat conduction,” International Journal of Heat & Mass Transfer, vol. 55, no. 17, pp. 4631-4637, 2012.

Z. T. Chen and K. Q. Hu, “Thermo-elastic analysis of a cracked half-plane under a thermal shock impact using the hyperbolic heat conduction theory,” Journal of Thermal Stresses, vol. 35, no. 4, pp. 342-362, 2012.

K. Q. Hu and Z. T. Chen, “Transient heat conduction analysis of a cracked half-plane using dual-phase-lag theory,” International Journal of Heat and Mass Transfer, vol. 62, no. 1, pp. 445-451, 2013.

M. Turkyilmazoglu, “Heat transfer from warm water to a moving foot in a footbath,” Applied Thermal Engineering, vol. 98, pp. 280-287, 2016.

M. Turkyilmazoglu, “Anomalous heat transfer enhancement by slip due to nanofluids in circular concentric pipes,” International Journal of Heat and Mass Transfer, vol. 85, pp. 609-614, 2015.

P. P. Teodorescu, Introduction to thermoelasticity, Beijin: Tsinghua University Press, 1989.

H. S. Carslaw and J. C. Jaeger, Conduction of heat in solids, Oxford University Press, 2 ed., 1986.

Y. Tanigawa, S. Kuriyama, and Y. Takeuti, “Transient thermal stress analysis of a strip with finite width under consideration of the heated boundary moving with constant velocity,” Transactions of the Japan Society of Mechanical Engineers Series A, vol. 51, no. 464, pp. 1042-1049, 1985.

Downloads

Published

2017-09-19

How to Cite

[1]
H. Kuanfang, Y. Qing, X. Dongming, and L. Xuejun, “Thermal Analysis of a Cracked Half-plane under Moving Point Heat Source”, Int. j. eng. technol. innov., vol. 7, no. 4, pp. 269–279, Sep. 2017.

Issue

Vol. 7 No. 4 (2017)

Section

Articles

License

Copyright (c) 2017 International Journal of Engineering and Technology Innovation

Creative Commons License

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

Copyright Notice

 

Submission of a manuscript implies: that the work described has not been published before that it is not under consideration for publication elsewhere; that if and when the manuscript is accepted for publication. Authors can retain copyright in their articles with no restrictions. Also, author can post the final, peer-reviewed manuscript version (postprint) to any repository or website.

 

 

Since Jan. 01, 2019, IJETI will publish new articles with Creative Commons Attribution Non-Commercial License, under Creative Commons Attribution Non-Commercial 4.0 International (CC BY-NC 4.0) License.

The Creative Commons Attribution Non-Commercial (CC-BY-NC) License permits use, distribution and reproduction in any medium, provided the original work is properly cited and is not used for commercial purposes.