Finite Element Analysis of a Novel Tensegrity-Based Vibratory Platform
DOI:
https://doi.org/10.46604/ijeti.2023.13230Keywords:
tensegrity, vibratory platform, vibratory conveyor, IronCAD, finite element analysisAbstract
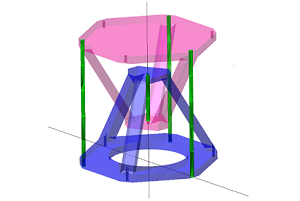
The study aims to conduct the finite element analysis (FEA) of a novel tensegrity-based vibratory platform by using IronCAD software. and analyze its deformation under external forces to verify if the platform can generate the required advancing motion. Firstly, the structure and operating principles of the proposed platform are introduced. Subsequently, individual parts are created using IronCAD software and assembled to form a solid model of the entire platform. Finally, employing Multiphysics for IronCAD, FEA is conducted to analyze the platform’s displacement under different external forces, as well as to examine its natural frequencies and mode shapes. The simulation results indicate that the proposed platform effectively moves a part in a specified direction. Additionally, the maximum stress remains below the yield strength. Moreover, the mode shapes corresponding to the initial 3 natural frequencies contribute to the advancing motion.
References
W. H. Hsieh and Adhitya, “On a Novel Micro Vibratory Platform with 3 DoFs,” Microsystem Technologies, vol. 28, no. 1, pp. 383-394, January 2022.
C, A. Kruelle, A. Götzendorfer, I. Rehberg, R. Grochowski, M. Rouijaa, and P. Walzel, “Granular Flow and Pattern Formation on a Vibratory Conveyor,” Traffic and Granular Flow’05, Springer Berlin Heidelberg, pp. 111-128, 2007.
G. Boothroyd, Assembly Automation and Product Design, 2nd ed., Florida: CRC Press, 2005.
W. H. Hsieh and N. N. Shih, “On an Inline Conveyor Resonantly Driven by Piezoelectric Actuators,” Journal of Vibroengineering, vol. 16, no. 5, pp. 2164-2170, August 2014.
R. B. Fuller, “Tensile-Integrity Structures,” U.S. Patent 3,063,521, 1962.
“Tensegrity,” https://en.wikipedia.org/wiki/Tensegrity, January 01, 2021.
“Tensegrity,” http://www.tensegriteit.nl/e-simple.html, June 01, 2021.
D. G. Emmerich, “Construction De Réseaux Autotendants,” French Patent 1,377,290, 1964.
K. Snelson, “Continuous Tension, Discontinuous Compression Structures,” U.S. Patent No. 3,169,611, 1965.
R. Motro, Tensegrity: Structural Systems for the Future, 1st ed., Amsterdam: Elsevier, 2003.
C. R. Calladine, “Buckminster Fuller’s “Tensegrity” Structures and Clerk Maxwell’s Rules for the Construction of Stiff Frames,” International Journal of Solids and Structures, vol. 14, no. 2, pp. 161-172, January 1978.
Z. Ji, M. Lin, and C. Chen, “Workspace Computation of a Tensegrity-Based Parallel Mechanism,” UPB Scientific Bulletin, Series D, vol. 80, no. 1, pp. 17-28, January 2018.
D. E. Ingber, “Tensegrity: The Architectural Basis of Cellular Mechanotransduction,” Annual Review of Physiology, vol. 59, no. 1, pp. 575-599, January 1997.
C. Sultan, “Tensegrity: 60 Years of Art, Science, and Engineering,” Advances in Applied Mechanics, vol. 43, pp. 69-145, January 2009.
R. Motro, “Tensegrity Systems: The State of the Art,” International Journal of Space Structures, vol. 7, no. 2, pp. 75-83, 1992.
I. J. Oppenheim and W. O. Williams, “Tensegrity Prisms as Adaptive Structures,” ASME International Mechanical Engineering Congress and Exposition, vol. 54, pp. 113-120, November 1997.
R. Skelton and C. Sultan, “Controllable Tensegrity: A New Class of Smart Structures,” Smart Structures and Materials 1997: Mathematics and Control in Smart Structures SPIE, vol. 3039, pp. 166-177, 1997.
C. Sultan, M. Corless, and R. T. Skelton, “Peak-to-Peak Control of an Adaptive Tensegrity Space Telescope,” Smart Structures and Materials 1999: Mathematics and Control in Smart Structures SPIE, vol. 3667, pp. 190-201, 1999.
C. Sultan, M. Corless, and R. E. Skelton, “Tensegrity Flight Simulator,” Journal of Guidance, Control, and Dynamics, vol. 23, no. 6, pp. 1055-1064, November-December 2000.
C. Paul, F. J. Valero-Cuevas, and H. Lipson, “Design and Control of Tensegrity Robots for Locomotion,” IEEE Transactions on Robotics, vol. 22, no. 5, pp. 944-957, October 2006.
A. G. Rovira and J. M. M. Tur, “Control and Simulation of a Tensegrity-Based Mobile Robot,” Robotics and Autonomous Systems, vol. 57, no. 5, pp. 526-535, May 2009.
T. M. Tran, “Reverse Displacement Analysis for Tensegrity Structures,” Ph.D. dissertation, University of Florida, Gainesville, Fla, USA, 2002.
M. Marshall, “Analysis of Tensegrity-Based Parallel Platform Devices,” Master thesis, University of Florida, Gainesville, Fla, USA, 2003.
A. Baker and C. D. Crane III, “Analysis of Three Degree of Freedom 6×6 Tensegrity Platform,” International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, vol. 2, pp. 31-37, September 2006.
S. M. M. Shekarforoush, M. Eghtesad, and M. Farid, “Kinematic and Static Analyses of Statically Balanced Spatial Tensegrity Mechanism with Active Compliant Components,” Journal of Intelligent & Robotic Systems, vol. 71, no. 3-4, pp. 287-302, September 2013.
J. M. McCarthy, “21st Century Kinematics: Synthesis, Compliance, and Tensegrity,” Journal of Mechanisms and Robotics-Transactions of the ASME, vol. 3, no. 2, article no. 020201, May 2011.
Y. X. Liu, Q. Bi, X. M. Yue, J. Wu, B. Yang, and Y. B. Li, “A Review on Tensegrity Structures-Based Robots,” Mechanism and Machine Theory, vol. 168, article no. 104571, February 2022.
Published
How to Cite
Issue
Section
License
Copyright (c) 2023 Wen-Hsiang Hsieh, Chen-Ji Pan, Yen-Chun Hsieh

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Copyright Notice
Submission of a manuscript implies: that the work described has not been published before that it is not under consideration for publication elsewhere; that if and when the manuscript is accepted for publication. Authors can retain copyright in their articles with no restrictions. Also, author can post the final, peer-reviewed manuscript version (postprint) to any repository or website.

Since Jan. 01, 2019, IJETI will publish new articles with Creative Commons Attribution Non-Commercial License, under Creative Commons Attribution Non-Commercial 4.0 International (CC BY-NC 4.0) License.
The Creative Commons Attribution Non-Commercial (CC-BY-NC) License permits use, distribution and reproduction in any medium, provided the original work is properly cited and is not used for commercial purposes.







.jpg)


