Dynamic Modeling of a Spatial Cable-Driven Continuum Robot Using Euler-Lagrange Method

Ammar Amouri; Chawki Mahfoudi; Abdelouahab Zaatri

doi:10.46604/ijeti.2020.4422

Authors

Ammar Amouri Department of Mechanical Engineering, Faculty of Technology Sciences, University of Brothers Mentouri, Constantine 1, Algeria
Chawki Mahfoudi Department of Mechanical Engineering, University Labri Ben M’Hidi, Oum el Bouaghi, Algeria
Abdelouahab Zaatri Independent Researcher, Ex-Department of Mechanical Engineering, University of Brothers Mentouri, Constantine 1, Algeria

DOI:

https://doi.org/10.46604/ijeti.2020.4422

Keywords:

continuum robot, cable-driven continuum robot, Taylor expansions approximations, Euler-Lagrange method, dynamic modeling

Abstract

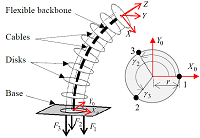
Continuum robots are kinematically redundant and their dynamic models are highly nonlinear. This study aims to overcome this difficulty by presenting a more practical dynamic model of a certain class of continuum robots called cable-driven continuum robot (CDCR). Firstly, the structural design of a CDCR with two rotational degrees of freedom (DOF) is introduced. Then, the kinematic models are derived according to the constant curvature assumption. Considering the complexity of the kinetic energy expression, it has been approximated by the well-known Taylor expansions. This case corresponds to weak bending angles within the specified bending angle range of the robot. On the other hand, due to the low weight of the CDCR components, the gravitational energy effects can be neglected compared to those stemmed from the elastic energy. Thereafter, the corresponding dynamic model is established using Euler-Lagrange method. Static and dynamic models have been illustrated by examples. This analysis and dynamic model development have been compared with the existing scientific literature. The obtained results shown that the consistency and the efficiency of accuracy for real-time have been carried out. However, the dynamic modeling of CDCR with more than 2-DOF leads to a more complex mathematical expression, and cannot be simplified by adopting the similar assumptions and methodology used in the case of 2-DOF.

References

L. Fryziel, “Modélisation et calibrage pour la commande d'un micro-robot continuum dédié à la chirurgie mini-invasive,” Ph.D. dissertation, Université Paris Est Créteil Val de Marne, France, December 2010.

D. Trivedi, C. D. Rahn, W. M. Kier, and I. D. Walker, “Soft robotics: biological inspiration, state of the art, and future research,” Applied Bionics and Biomechanics, vol. 5, no. 3, pp. 99-117, 2008.

G. Robinson and J. B. C. Davies, “Continuum robots - a state of the art,” Proc.IEEE International Conference on Robotics and Automation, Detroit, Michigan, May 1999, pp. 2849-2854.

G. S. Chirikjian and J. W. Burdick, “A modal approach to hyper-redundant manipulator kinematics,” IEEE Transactions on Robotics and Automation, vol. 10, no. 3, pp. 343-354, June 1994.

T. M. Bieze, “Contribution to kinematic modeling and control of soft manipulators using computational mechanics,” Ph.D. dissertation, Université des Sciences et Technologies de Lille, France, October 2017.

R. Cieslak and A.Morecki, “Elephant trunk type elastic manipulator a tool for bulk and liquid type materials transportation,” Robotica, vol. 17, no. 1, pp. 11-16, January 1999.

I. D. Walker and M. W. Hannan, “A novel elephant's trunk' robot,” Proc. IEEE/ASME International Conference on Advanced Intelligent Mechatronics, September 1999, pp. 410-415.

O. Lakhal, “Contribution to the modeling and control of hyper-redundant robots: application to additive manufacturing in the construction,” Ph.D. dissertation, Université des Sciences etTechnologies de Lille, France, January 2019.

W. McMahan, B. A. Jones, and I. D. Walker, “Design and implementation of a multi-section continuum robot: Air-Octor,” Proc. IEEE International Conference on Intelligent Robots and Systems, August 2005, pp. 2578-2585.

W. McMahan and I. D. Walker, “Octopus-inspired grasp-synergies for continuum manipulators,” Proc. IEEE International Conference on Robotics and Biomimetics, February 2009, pp.945-950.

S. Mosqueda, Y. Moncada, C. Murrugarra, and H. Leon-Rodriguez, “Constant curvature kinematic model analysis and experimental validation for tendon driven continuum manipulators,” Proc. the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018), vol. 2, 2018, pp.211-218.

Y. Tian, M. Luan, X. Gao, W. Wang, and L. Li, “Kinematic analysis of continuum robot consisted of driven flexible rods,” Mathematical Problems in Engineering, vol. 2016, pp. 1-7, 2016.

J. Tang, Y. Zhang, F. Huang, J. Li, Z. Chen, W. Song, S. Zhu, and J. Gu, “Design and kinematic control of the cable-driven hyper-redundant manipulator for potentialunderwater applications,” Applied Sciences, vol. 9, no. 6, pp. 1-20, 2019.

A. K. Mishra, A. Mondini, E. Del Dottore, A. Sadeghi, F. Tramacere, and B. Mazzolai, “Modular continuum manipulator: Analysis and characterization of its basic module,” Biomimetics, vol. 3, no. 1, pp. 1-16, 2018.

B. He, Z. Wang, Q. Li, H. Xie, and R. Shen, “An analytic method for the kinematics and dynamics of a multiple-backbone continuum robot,” International Journal of Advanced Robotic Systems, vol. 10, pp. 1-13, 2013.

A. Amouri, C. Mahfoudi, A. Zaatri, O. Lakhal, and R. Merzouki, “A metaheuristic approach to solve inverse kinematics of continuum manipulators,” Journal of systems and Control Engineering, vol. 231, no. 5, pp. 380-394, 2017.

H. El-Hussieny, S. G. Jeong, and J. H. Ryu, “Dynamic modeling of a class of soft growing robots using Euler-Lagrange formalism,” Proc. the SICE Annual Conference, Society of Instrument and Control Engineers (SICE), Hiroshima, Japan, September 10-13, 2019.

R. J. Webster and B. A. Jones, “Design and kinematic modeling of constant curvature continuum robots: A review,” International Journal of Robotics Research, vol. 29, no. 13, pp. 1661-1683, 2010.

V. Falkenhahn, T Mahl, A. Hildebrandt, A. Hildebrandt, R. Neumann, and O. Sawodny, “Dynamic modeling of bellows-actuated continuum robots using the Euler-Lagrange formalism,” IEEE Transactions on Robotics, vol. 31, no. 6, pp. 1483-1496, December 2015.

D. C. Rucker and R. J. Webster III, “Statics and dynamics of continuum robots with general tendon routing and external loading,” IEEE Transactions on Robotics, vol.27, no. 6, pp. 1033-1044, July 2011.

A. Abu Alqumsan, S. Khoo, and M. Norton, “Robust control of continuum robots using Cosserat rod theory,” Mechanism and Machine Theory, vol. 131, pp. 48-61, January 2019.

F. Renda, F. Boyer, J. Dias, and L.Seneviratne, “Discrete Cosserat approach for multisection soft manipulator dynamics,” IEEE Transactions on Robotics, vol. 34, no. 6, 2018.

F. Matsuno and H. Sato, “Trajectory tracking control of snake robots based on dynamic model,” In: Proc. IEEE International Conference of Robotics and Automation, Barcelona, Spain, April 2005, pp. 3040-3045.

A. Gravagne, C. D. Rahn, and I. D. Walker, “Large deflection dynamics and control for planar continuum robots,” IEEE/ASME Transactions on Mechatronics, vol. 8, no. 2, pp. 299-307, 2003.

W. Rone and P.Ben-Tzvi, “Continuum robot dynamics utilizing the principle of virtual power,” IEEE Transactions on Robotics, vol. 30, no. 1, pp. 275-287, February 2014.

W. Rone and P. Ben-Tzvi, “Mechanics modeling of multi-segment rod-driven continuum robots,” Journal of Mechanisms and Robotics,” vol. 6, no. 4, November 2014.

A. Amouri, A. Zaatri, and C. Mahfoudi, “Dynamic modeling of a class of continuum manipulators in fixed orientation,” Journal of Intelligent and Robotic Systems, vol. 91, no. 3-4, pp. 413-424, 2018.

M. Dehghani and S. Ali A.Moosavian, “Dynamics modeling of a continuum robotic arm with a contact point in planar grasp,” Journal of Robotics, vol. 2014, Article ID 308283, 2014.

D. G. Fertis, “Advanced mechanics of structure,” Marcel Dekker, Inc., New York City, 1996.