A New 6D Chaotic Generator: Computer Modelling and Circuit Design
DOI:
https://doi.org/10.46604/ijeti.2022.9601Keywords:
chaotic behavior, chaos generator, computer simulation, circuit simulationAbstract
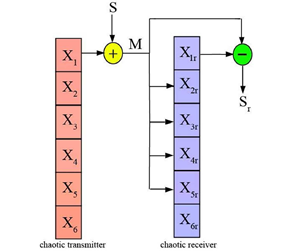
The objective of this study aims at using the Matlab-Simulink environment and the LabVIEW software environment to build computer models of a six-dimensional (6D) chaotic dynamic system. For the fixed system’s parameters, the spectrum of Lyapunov exponents and the Kaplan-York dimension are calculated. The presence of two positive Lyapunov exponents demonstrates the hyperchaotic behavior of the system. The fractional Kaplan-York dimension indicates the fractal structure of strange attractors. An active control method is extended to achieve global chaotic synchronization of two identical novel 6D chaotic systems with unknown system parameters. Based on the results obtained in Matlab-Simulink and LabVIEW models, a chaotic signal generator for the 6D chaotic system is implemented in the MultiSim environment. The experimental results show that the chaotic behavior simulation in the MultiSim environment is similar to those in the Matlab-Simulink and LabVIEW models. The simulation results demonstrate that the Pecora-Carroll method is a simple way of chaotic masking and signal decoding.
References
F. Yu, et al., “Secure Communication Scheme Based on a New 5D Multistable Four-Wing Memristive Hyperchaotic System with Disturbance Inputs,” Complexity, vol. 2020, pp. 1-16, January 2020.
A. Ouannas, et al., “A Novel Secure Communications Scheme Based on Chaotic Modulation, Recursive Encryption and Chaotic Masking,” Alexandria Engineering Journal, vol. 60, no. 1, pp. 1873-1884, December 2020.
S. Wang, et al., “An Image Encryption Algorithm Based on a Hidden Attractor Chaos System and the Knuth-Durstenfeld Algorithm,” Optics and Lasers in Engineering, vol. 128, Article no. 105995, May 2020.
A. Sambas, et al., “A 3-D Multi-Stable System with a Peanut-Shaped Equilibrium Curve: Circuit Design, FPGA Realization, and an Application to Image Encryption,” IEEE Access, vol. 8, pp. 137116-137132, July 2020.
S. Vaidyanathan, et al., “A New Biological Snap Oscillator: Its Modelling, Analysis, Simulations and Circuit Design,” International Journal of Simulation and Process Modelling, vol. 13, no. 5, pp. 419-432, January 2018.
E. N. Lorenz, “Deterministic Non-Periodic Flow,” Journal of the Atmospheric Sciences, vol. 20, pp. 130-142, March 1963.
K. M. Cuomo, et al., “Circuit Implementation of Synchronized Chaos with Applications to Communications,” Physical Review Letters, vol. 71, no. 1, pp. 65-68, August 1993.
K. M. Ibrahim, et al., “Chaotic Behavior of the Rossler Model and Its Analysis by Using Bifurcations of Limit Cycles and Chaotic Attractors,” Journal of Physics: Conference Series, vol. 1003, no. 1, Article no. 012099, May 2018.
Y. Y. Hou, et al., “Rikitake Dynamo System, Its Circuit Simulation and Chaotic Synchronization via Quasi-Sliding Mode Control,” TELKOMNIKA Telecommunication, Computing, Electronics, and Control, vol. 19, no. 4, pp. 1428-1438, August 2021.
F. Hannachi, “Analysis, Dynamics and Adaptive Control Synchronization of a Novel Chaotic 3D System,” SN Applied Sciences, vol. 1, no. 2, Article no. 158, February 2019.
I. Pehlivan, et al., “A New Chaotic Attractor from General Lorenz System Family and Its Electronic Experimental Implementation,” Turkish Journal of Electrical Engineering and Computer Sciences, vol. 18, no. 2, pp. 171-184, March 2010.
Q. H. Alsafasfeh, et al., “A New Chaotic Behavior from Lorenz and Rossler Systems and Its Electronic Circuit Implementation,” Circuits and Systems, vol. 2, no. 2, pp. 101-105, April 2011.
S. Vaidyanathan, et al., “Analysis, Adaptive Control and Synchronization of a Seven-Term Novel 3D Chaotic System with Three Quadratic Nonlinearities and Its Digital Implementation in LabVIEW,” Journal of Engineering Science and Technology Review, vol. 8, no. 2, pp. 130-141, April 2015.
A. Sambas, et al., “Dynamics, Circuit Design and Fractional-Order Form of a Modified Rucklidge Chaotic System,” Journal of Physics: Conference Series, vol. 1090, no. 1, Article no. 012038, September 2018.
F. Q. Wang, et al., “Hyperchaos Evolved from the Liu Chaotic System,” Chinese Physics B, vol. 15, no. 5, pp. 963-968, May 2006.
M. W. Luo, et al., “Circuitry Implementation of a Novel Four-Dimensional Nonautonomous Hyperchaotic Liu System and Its Experimental Studies on Synchronization Control,” Chinese Physics B, vol. 18, no. 6, pp. 2168-2175, June 2009.
J. Lu, et al., “The Compound Structure of a New Chaotic Attractor,” Chaos, Solitons, and Fractals, vol. 14, no. 5, pp. 669-672, September 2002.
L. Xiong, et al., “Dynamical Analysis, Synchronization, Circuit Design, and Secure Communication of a Novel Hyperchaotic System,” Complexity, vol. 2017, Article no. 4962739, 2017.
L. Xiong, et al., “Circuit Implementation and Antisynchronization of an Improved Lorenz Chaotic System,” Shock and Vibration, vol. 2016, Article no. 1617570, 2016.
S. Vaidyanathan, et al., “Analysis, Control, Synchronization and SPICE Implementation of a Novel 4D Hyperchaotic Rikitake Dynamo System without Equilibrium,” Journal of Engineering Science and Technology Review, vol. 8, no. 2, pp. 232-244, April 2015.
S. Vaidyanathan, et al., “A 5D Hyperchaotic Rikitake Dynamo System with Hidden Attractors,” The European Physical Journal Special Topics, vol. 224, pp. 1575-1592, July 2015.
S. Vaidyanathan, et al., “A 5D Multi-Stable Hyperchaotic Two-Disk Dynamo System with no Equilibrium Point: Circuit Design, FPGA Realization and Applications to TRNGs and Image Encryption,” IEEE Access, vol. 9, pp. 81352-81369, June 2021.
E. Tlelo-Cuautle, et al., Optimization of Integer/Fractional Order Chaotic Systems by Metaheuristics and Their Electronic Realization, Boca Raton: CRC Press, 2021.
M. I. Kopp, et al., “Magnetic Convection in a Nonuniformly Rotating Electroconducting Medium,” Journal of Experimental and Theoretical Physics, vol. 127, no. 6, pp. 1173-1196, July 2018.
G. Benettin, et al., “Lyapunov Characteristic Exponents for Smooth Dynamical Systems and for Hamiltonian Systems: A Method for Computing All of Them,” Meccanica, vol. 15, no. 1, pp. 9-20, March 1980.
A. Wolf, et al., “Determining Lyapunov Exponents from a Time Series,” Physica D: Nonlinear Phenomena, vol. 16, no. 3, pp. 285-317, July 1985.
M. Sandri, “Numerical Calculation of Lyapunov Exponents,” The Mathematica Journal, vol. 6, pp. 78-84, January 1996.
H. Binous, et al., “An Improved Method for Lyapunov Exponents Computation,” https://library.wolfram.com/infocenter/MathSource/7109/, March 09, 2008.
L. M. Pecora, et al., “Synchronization in Chaotic Systems,” Physical Review Letters, vol. 64, no. 8, pp, 821-824, March 1990.
R. W. Larsen, LabVIEW for Engineers, Upper Saddle River: Prentice Hall, 2011.
Published
How to Cite
Issue
Section
License
Copyright Notice
Submission of a manuscript implies: that the work described has not been published before that it is not under consideration for publication elsewhere; that if and when the manuscript is accepted for publication. Authors can retain copyright in their articles with no restrictions. Also, author can post the final, peer-reviewed manuscript version (postprint) to any repository or website.

Since Jan. 01, 2019, IJETI will publish new articles with Creative Commons Attribution Non-Commercial License, under Creative Commons Attribution Non-Commercial 4.0 International (CC BY-NC 4.0) License.
The Creative Commons Attribution Non-Commercial (CC-BY-NC) License permits use, distribution and reproduction in any medium, provided the original work is properly cited and is not used for commercial purposes.







.jpg)


