Vibration Analysis of Thermoelastic Micro Beam with Double Porosity Structure
Keywords:
Double porosity, thermoelasticity, Lord-Shulman theory, microbeam, sinusoidal pulse heatingAbstract
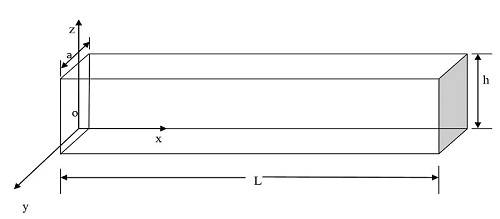
The present investigation is concerned with vibration analysis of a homogeneous, isotropic thermo elastic micro beam with double porosity structure subjected to sinusoidal pulse heating. Lord-Shulman [1] theory of thermo elasticity with one relaxation time is used to solve the problem. Laplace transform technique has been used to obtain the expressions for lateral deflection, axial stress, axial displacement, volume fraction field and temperature distribution. A numerical inversion technique has been applied to recover the resulting quantities in the physical domain. Variations of axial displacement, axial stress, lateral deflection, volume fraction field and temperature distribution against axial distance are depicted graphically to show the effect of porosity and relaxation time parameters. Some particular cases are also deduced.
References
H. Lord and Y. Shulman, “A generalized dynamical theory of thermo elasticity,” Journal of Mechanics and Physics of Solids, vol. 15, pp. 299-309, 1967.
M. A. Biot, “General theory of three-dimensional consolidation,” Journal of Applied Physics, vol. 12, pp. 155-164, 1941.
G. I. Barenblatt, I. P. Zheltov, and I. N. Kochina, “Basic concept in the theory of seepage of homogeneous liquids in fissured rocks (strata),” Journal of Applied Mathematics and Mechanics, vol. 24, pp. 1286-1303, 1960.
E. C. Aifantis, “Introducing a multi-porous medium,” Developments in Mechanics, vol. 8, pp. 209-211, 1977.
E. C. Aifantis, “On the response of fissured rocks,” Developments in Mechanics, vol. 10, pp. 249-253, 1979.
E. C. Aifantis, “On the problem of diffusion in solids,”Acta Mechanica, vol. 37, pp. 265-296, 1980.
R. K. Wilson and E .C. Aifantis, “On the theory of consolidation with double porosity,” International Journal of Engineering Science, vol. 20, no. 9, pp. 1009-1035, 1984.
M. Y. Khaled, D. E. Beskos and E. C. Aifantis, “On the theory of consolidation with double porosity-III,” International Journal of Numerical and Analytical Methods in Geomechanics, vol. 8, pp. 101-123, 1984.
D. E. Beskos and E. C. Aifantis, “On the theory of consolidation with double porosity-II,” International Journal of Engineering Science, vol. 24, pp. 1697-1716, 1986.
N. Khalili and A. P. S. Selvadurai, “A fully coupled constitutive model for thermo-hydro –mechanical analysis in elastic media with double porosity,” Geophysical Research Letters, vol. 30, pp. 2268-2271, 2003.
M. Svanadze, “Fundamental solution in the theory of consolidation with double porosity,” Journal of the Mechanical Behavior of Materials, vol. 16, pp. 123-130, 2005.
M. Svanadze, “Plane waves and boundary value problems in the theory of elasticity for solids with double porosity,” Acta Applicande Mathematicae, vol. 122, pp. 461-470, 2012.
B. Straughan, “Stability and uniqueness in double porosity elasticity,” International Journal of Engineering Science, vol. 65, pp. 1-8, 2013.
J. W. Nunziato and S. C. Cowin, “A nonlinear theory of elastic materials with voids,” Archives of Rational Mechanics and Analysis, vol. 72, pp. 175-201, 1979.
S. C. Cowin and J .W. Nunziato, “Linear elastic materials with voids,” Journal of Elasticity, vol. 13, pp. 125-147, 1983.
D. Iesan and R. Quintanilla, “On a theory of thermo elastic materials with a double porosity structure,” Journal of Thermal Stresses, vol. 37, pp. 1017-1036, 2014.
A. Dimarogonas, Vibration for engineers. Prentice-Hall, Inc., 2nd edition, 1996.
L. Meirovitch, Fundamentals of vibrations. McGraw-Hill, International Edition, 2001.
B. A. Boley, “Approximate analyses of thermally induced vibrations of beams and plates,” Journal of Applied Mechanics, vol. 39, pp. 212-216, 1972.
G. D. Manolis and D. E. Beskos, “Thermally induced vibrations of beam structures,” Computer Methods in Applied Mechanics and Engineering, vol. 21, pp. 337-355, 1980.
N. S. Al-Huniti, M. A. Al-Nimr, and M. Naij, “Dynamic response of a rod due to a moving heat source under the hyperbolic heat conduction model,” Journal of Sound and Vibration, vol. 242, pp. 629-640, 2001.
B. Biondi and S. Caddemi, “Closed form solutions of Euler-Bernoulli beams with singularities,” International Journal of Solids and Structures, vol. 42, pp. 3027-3044, 2005.
D. N. Fang, Y. X. Sun, and A. K. Soh, “Analysis of frequency spectrum of laser-induced vibration of microbeam resonators,” Chinese Physics Letters, vol. 23, pp. 1554-1557, 2006.
J. N. Sharma, and D. Grover, “Thermo elastic vibrations in micro-/nano-scale beam resonators with voids,” Journal of Sound and Vibration, vol. 330, pp. 2964-2977, 2011.
I. Esen, “A new FEM procedure for transverse and longitudinal vibration analysis of thin rectangular plates subjected to a variable velocity moving load along an arbitrary trajectory,” Latin American Journal of Solids and Structures, vol. 12, pp. 808-830, 2015.
A. M. Dehrouyeh-Semnani, M. Dehrouyeh, M. Torabi-Kafshgari, and M. Nikkah-Bahrami, “A damped sandwich beam model based on symmetric-deviatoriccouple stress theory,” International Journal of Engineering Science, vol. 92, pp. 83-94, 2015.
A. M. Dehrouyeh-Semnani, M. Dehrouyeh, M. Torabi-Kafshgari, and M. Nikkah-Bahrami, “Free flexural vibration of geometrically imperfect functionally graded microbeams,” International Journal of Engineering Science, vol. 105, pp. 56-79, 2016.
M. Mojahedi, and M. Rahaeifard, “A size-dependent model for coupled 3D deformations of nonlinear microbridges,” International Journal of Engineering Science, vol. 100, pp. 171-182, 2016.
G. Honig, and U. Hirdes, “A method for the numerical inversion of the Laplace transforms,” Journal of Computational and Applied Mathematics, vol. 10, pp. 113-132, 1984.
D. Tzou, Macro-to-Micro Heat transfer, Taylor& Francis, Washington DC, 1996.
H. Sherief, and H. Saleh, “A half space problem in the theory of generalized thermo elastic diffusion,” International Journal of Solids and Structures. vol. 42, pp. 4484-4493, 2005.
N. Khalili, “Coupling effects in double porosity media with deformable matrix,” Geophysical Research Letters, vol. 30, no. 22, pp. 2153, doi: 10.1029/2003GL018544, 2003.
A. Altinörs, and Halilönder, “A double-porosity model for a fractured aquifer with non-darcian flow in fractures,” Hydrological Sciences-Journal-des Sciences Hydrologiques, vol. 53, no. 4, pp. 868-882, 2008.
A. R. Bagherieh, N. Khalili, G. Habibagahi, and A. Ghahramani, “Drying response and effective stress in a double porosity aggregated soil,” Engineering Geology, vol. 105, pp. 44-50, 2009.
T. D. Tran Ngo, J. Lewandowska and H. Bertin, “Experimental evidence of the double-porosity effects in geomaterials,”Acta Geophysica, vol. 62, no. 3, pp. 642-655, 2014.
Published
How to Cite
Issue
Section
License
Copyright (c) 2017 International Journal of Engineering and Technology Innovation

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Copyright Notice
Submission of a manuscript implies: that the work described has not been published before that it is not under consideration for publication elsewhere; that if and when the manuscript is accepted for publication. Authors can retain copyright in their articles with no restrictions. Also, author can post the final, peer-reviewed manuscript version (postprint) to any repository or website.

Since Jan. 01, 2019, IJETI will publish new articles with Creative Commons Attribution Non-Commercial License, under Creative Commons Attribution Non-Commercial 4.0 International (CC BY-NC 4.0) License.
The Creative Commons Attribution Non-Commercial (CC-BY-NC) License permits use, distribution and reproduction in any medium, provided the original work is properly cited and is not used for commercial purposes.


.jpg)


